

|
Edward Lowton
Editor |


|
| Home> | Plant, Process & Control | >Pumps | >Go with the flow for measurement |
ARTICLE
Go with the flow for measurement
25 January 2013
A basic understanding of flow calculations and estimates makes sizing valves a much simpler process, as John Baxter, of Swagelok explains Valve size often is described by the nominal size of the end connections but a m
A basic understanding of flow calculations and estimates
makes sizing valves a much simpler process, as John Baxter,
of Swagelok explains
Valve size often is described by the nominal size of the end connections but a more important measure is the flow that the valve can provide. Using the principles of flow calculations, some basic formulas, and the effects of specific gravity and temperature, flow can be estimated well enough to easily select a valve size.
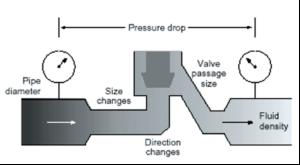
Flow Calculation Principles We need to know only the size and shape of the orifice, the diameter of the pipe, and the fluid density.We can then calculate the flow rate for any value of pressure drop across the orifice (the difference between inlet and outlet pressures). (Fig. 1) We also need to know the pressure drop and the fluid density as well as all the valve passage dimensions and all the changes in size and direction of flow through the valve.
However, rather than doing complex calculations, we use the valve flow coefficient, which combines the effects of all the flow restrictions in the valve into a single number (Fig. 2).
Valve manufacturers determine the valve flow coefficient by testing the valve with water at several flow rates, using a standard test method developed by the Instrument Society of America for control valves and now used widely for all valves.
Flow tests are done in a straight piping system of the same size as the valve, so that the effects of fittings and piping size changes are not included.
Liquid Flow Because liquids are incompressible fluids, their flow rate depends only on the difference between the inlet and outlet pressures (?p pressure drop). The flow is the same whether the system pressure is low or high, so long as the difference between the inlet and outlet pressures is the same.
Gas Flow Gas flow calculations are slightly more complex because gases are compressible fluids whose density changes with pressure.
In addition, there are two conditions that must be considered—low-pressure drop flow and high-pressure drop flow.
When outlet pressure (p2) is less than half of inlet pressure (p1)—high pressure drop— any further decrease in outlet pressure does not increase the flow because the gas has reached sonic velocity at the orifice, and it cannot break that 'sound barrier'.
The equation for high-pressure drop flow is simpler because it depends only on inlet pressure and temperature, valve flow coefficient, and specific gravity of the gas.
Effects of Specific Gravity The flow equations include the variables liquid specific gravity (Gf) and gas specific gravity (Gg), which are the density of the fluid compared to the density of water (for liquids) or air (for gases).
However, specific gravity is not accounted for in the graphs, so a correction factor must be applied, which includes the square root of G. Taking the square root reduces the effect and brings the value much closer to that of water or air, 1.0.
The effect of specific gravity on gases is similar. Only gases with very low or very high specific gravity change the flow by more than 10% from that of air.
Effects of Temperature Temperature usually is ignored in liquid flow calculations because its effect is too small.
Temperature has a greater effect on gas flow calculations, because gas volume expands with higher temperature and contracts with lower temperature. But similar to specific gravity, temperature affects flow by only a square-root factor. The plus-or-minus 10 percent range covers the usual operating temperatures of most common applications.
Cited References 1. ISA S75.01, Flow Equations for Sizing Control Valves, Standards and Recommended Practices for Instrumentation and Control, 10th ed., Vol. 2, 1989.
2. ISA S75.02, Control Valve Capacity Test Procedure, Standards and Recommended Practices for Instrumentation and Control, 10th ed., Vol. 2, 1989.
Valve size often is described by the nominal size of the end connections but a more important measure is the flow that the valve can provide. Using the principles of flow calculations, some basic formulas, and the effects of specific gravity and temperature, flow can be estimated well enough to easily select a valve size.
Flow Calculation Principles We need to know only the size and shape of the orifice, the diameter of the pipe, and the fluid density.We can then calculate the flow rate for any value of pressure drop across the orifice (the difference between inlet and outlet pressures). (Fig. 1) We also need to know the pressure drop and the fluid density as well as all the valve passage dimensions and all the changes in size and direction of flow through the valve.
However, rather than doing complex calculations, we use the valve flow coefficient, which combines the effects of all the flow restrictions in the valve into a single number (Fig. 2).
Valve manufacturers determine the valve flow coefficient by testing the valve with water at several flow rates, using a standard test method developed by the Instrument Society of America for control valves and now used widely for all valves.
Flow tests are done in a straight piping system of the same size as the valve, so that the effects of fittings and piping size changes are not included.
Liquid Flow Because liquids are incompressible fluids, their flow rate depends only on the difference between the inlet and outlet pressures (?p pressure drop). The flow is the same whether the system pressure is low or high, so long as the difference between the inlet and outlet pressures is the same.
Gas Flow Gas flow calculations are slightly more complex because gases are compressible fluids whose density changes with pressure.
In addition, there are two conditions that must be considered—low-pressure drop flow and high-pressure drop flow.
When outlet pressure (p2) is less than half of inlet pressure (p1)—high pressure drop— any further decrease in outlet pressure does not increase the flow because the gas has reached sonic velocity at the orifice, and it cannot break that 'sound barrier'.
The equation for high-pressure drop flow is simpler because it depends only on inlet pressure and temperature, valve flow coefficient, and specific gravity of the gas.
Effects of Specific Gravity The flow equations include the variables liquid specific gravity (Gf) and gas specific gravity (Gg), which are the density of the fluid compared to the density of water (for liquids) or air (for gases).
However, specific gravity is not accounted for in the graphs, so a correction factor must be applied, which includes the square root of G. Taking the square root reduces the effect and brings the value much closer to that of water or air, 1.0.
The effect of specific gravity on gases is similar. Only gases with very low or very high specific gravity change the flow by more than 10% from that of air.
Effects of Temperature Temperature usually is ignored in liquid flow calculations because its effect is too small.
Temperature has a greater effect on gas flow calculations, because gas volume expands with higher temperature and contracts with lower temperature. But similar to specific gravity, temperature affects flow by only a square-root factor. The plus-or-minus 10 percent range covers the usual operating temperatures of most common applications.
Cited References 1. ISA S75.01, Flow Equations for Sizing Control Valves, Standards and Recommended Practices for Instrumentation and Control, 10th ed., Vol. 2, 1989.
2. ISA S75.02, Control Valve Capacity Test Procedure, Standards and Recommended Practices for Instrumentation and Control, 10th ed., Vol. 2, 1989.
MORE FROM THIS COMPANY
OTHER ARTICLES IN THIS SECTION

















